
This is an example of a shader with a few different inputs with meta data. The script below creates the Mandelbrot Set shader.
// The obvious piece of programmer art in any OSL intro is a Mandelbrot shader
shader Mandelbrot(
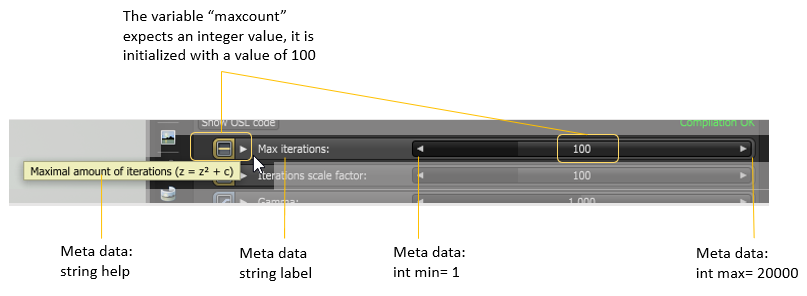
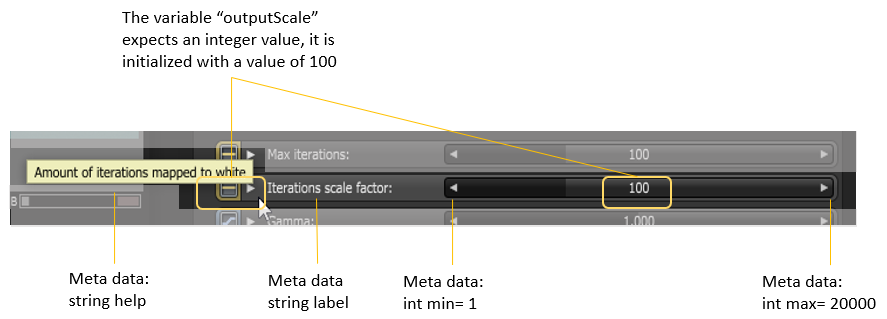
output color c = 0,int maxcount = 100[[int min=1, int max=20000, int sliderexponent=4,string label = "Max iterations",string help = "Maximal amount of iterations (z = z² + c)"]],int outputScale = 100[[int min=1, int max=20000, int sliderexponent=4,string label = "Iterations scale factor",string help = "Amount of iterations mapped to white"]],float gamma = 1.0[[float min=0.1, float max=10, int sliderexponent=4,string label = "GammaThe function or attribute used to code or decode luminance for common displays. The computer graphics industry has set a standard gamma setting of 2.2 making it the most common default for 3D modelling and rendering applications.",string help = "Gamma value applied to the gradient"]],point projection = 0[[string label = "Projection"]],matrix xform = matrix(.33333, 0, 0, -.5, 0, .33333, 0, -.33333, 0, 0, .33333, 0, 0, 0, 0, 1)[[string label = "UV transform", int dim = 2]],int smooth = 0[[string widget="checkBox",string label = "Smooth gradient",string help = "Smooth out the gradient outside the Mandelbrot set"]]
)
{
point p = transform(1 / xform, projection);float cx = (p[0]-.5);float cy = (p[1]-.5);float x = cx;float y = cy;float prevRR = 0;float rr = x*x + y*y;int count = 0;while (rr < 4 && count < maxcount){count += 1;// z = z² + cfloat x2 = x*x - y*y + cx;y = 2*x*y + cy;x = x2;prevRR = rr;rr = x*x + y*y;}if (count < maxcount){float h = (float)count;if (smooth){h = h + (4 - prevRR) / (rr - prevRR);}c = pow(h / outputScale, gamma);c = min(c, .999);}else{c = 1.0;}
}
The Mandelbrot set is a famous example of a fractal in mathematics, it is one of the first images generated in computer graphics that displayed a fractal geometric shape. It showed how visual complexity can be created from simple rules and that a degree of order is present in things that are considered messy or chaotic (like clouds or shorelines).
The computer graphic image was created by applying the common fractal equation Zn+1=Zn2+c to each pixel in an iterative process. In that equation, c and z are complex numbers, and n is zero or a positive integer (natural number). Starting with z0=0, c is in the Mandelbrot set if the absolute value of zn never becomes larger than a certain number (that number depends on c), no matter how large n gets. The resulting image became known as the Mandelbrot set.

Figure 1: The Mandelbrot set
Therefore, the purpose of the Mandelbrot Set shader is to recreate the Mandelbrot set fractal procedurally wiht an OSL script and allow the resulting image to display on a surface when the shader is used on a material for that surface (Figure 2).

Figure 2: The Mandelbrot Set displayed on a cube surface
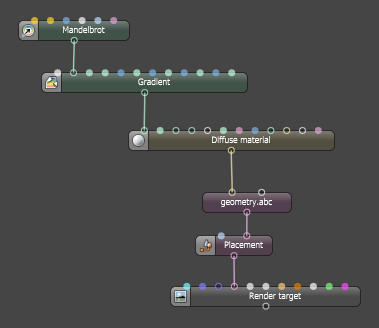
Figure 3: The Mandelbrot Set shader plugged into the Gradient node's Texture input pin


Figure 4: The Mandelbrot Shader implemented with an Octane OSL Texture node

Figure 5: Declaration and Function Body
Line 1: This is a note for viewers of the code, it is ignored by the compiler.
Line 3: This names the OSL texture node.

Figure 6: OSL texture node
Line 4: An OSL texture requires one output attribute, so this is provided by the declaration of the variable c, which is of OSL I/O type color corresponding to an Octane Texture attribute node.
Lines 5 - 8: This declares input of OSL I/O type int corresponding to an Octane Int attribute node (1D-value)
Lines 9 - 12: This declares input of OSL I/O type “int” corresponding to an Octane Int attribute node (1D-value)
Line 27: Gets a point. This implements the usual UV transform and Projection inputs of Octane texture nodes.
Lines 28 - 34: A few more local variables to hold values needed in the function body. The variable P holds the pixel value, which is taken from the transform matrix provided through Line 19.
Lines 35 - 44: These are the iterations that results in a fractal shape. Each iteration is checked.
Lines 46 - 59 : This outputs the value 1.0 if the iteration doesn't diverge, and this outputs less than 1.0 if the iteration diverged at some point.