
The microfacet BRDFs were implemented as part of the OSL materials to support the default microfacet BRDF closures in OSL. They are also useful for importing materials from other applications because microfacet models (especially GGX) are widely adopted across different applications. With the BRDF models integrated in the OctaneRender® core, OctaneRender® achieves a similar look from importing materials.
The original OctaneRender® BRDF is done by doing the BRDF sampling based on the light direction. In the additional BRDF models, the BRDF sampling is done based on the microfacet normal. These microfacet models try to mimic the surface's roughness, reconstructing the surface bumpiness at the microgeometry level and enabling the render core to achieve material properties like Glossy Fresnel, which reduces the fresnel effect at grazing angles for high roughness surfaces. These additional models also allow anisotropic roughness, which help simulates anisotropic surface reflectance.
The most obvious difference between the three additional microfacet models is the specular highlight lobe, defined by the microfacet NDF (normal distribution function), the roughness controls the lobe size using this NDF, similar to how OctaneRender's existing BRDF works (but without NDF). The Ward BRDF behaves similar to the Beckmann BRDF model, but is considered to be cheaper to evaluate. While GGX is visually different compared to the two and is known for a longer specular tail.

Figure 1: Comparison of microfacet BRDFs with a Roughness of 0.2
With a Roughness value of 0.2, the difference between Ward and Beckmann is small, while GGX's lobe is quite different. GGX's lobe tends to have a longer tail near the end of the specular highlight compared to both Ward and Beckmann BRDF.

Figure 2: Comparison of microfacet BRDFs with a Roughness of 0.5
With a Roughness value of 0.5, the difference between Ward and Beckmann are still very similar, while GGX's lobe remains to be very different from the two. Just as the above case, GGX's specular highlight spreads out more due to the longer tail, thus appears to be brighter in areas around the reflection of the direct light.
To see why this is the case, below is a logarithmic graph of GGX's and Beckmann's NDFs, given their Roughness (0.2) with varying angle of surface normal and microfacet normal. This shows the teal curve (GGX) has a higher NDF value once the angle between surface normal and microfacet normal is greater than 37.5 degrees and never really gets down to 0, unlike the Beckmann's NDF, which goes to 0 before reaching 45 degrees (Figure 3).

Figure 3: Logarithmic graph of NDF at roughness = 0.2, X-axis represents the angle between surface normal and microfacet normal (half vector), Y-axis represents the logarithmic of the resulting NDF
For the sake of comparison at a different roughness level, below is the same graph but with roughness = 0.5. The main difference here is that both BRDFs now have a less bright but a wider specular highlight lobe, however this does not change the fact that the GGX's specular tail is longer than the Beckmann, as its NDF never goes to 0 in the hemisphere, while Beckmann's specular tail quickly goes to 0 after 45 degrees (Figure 4).
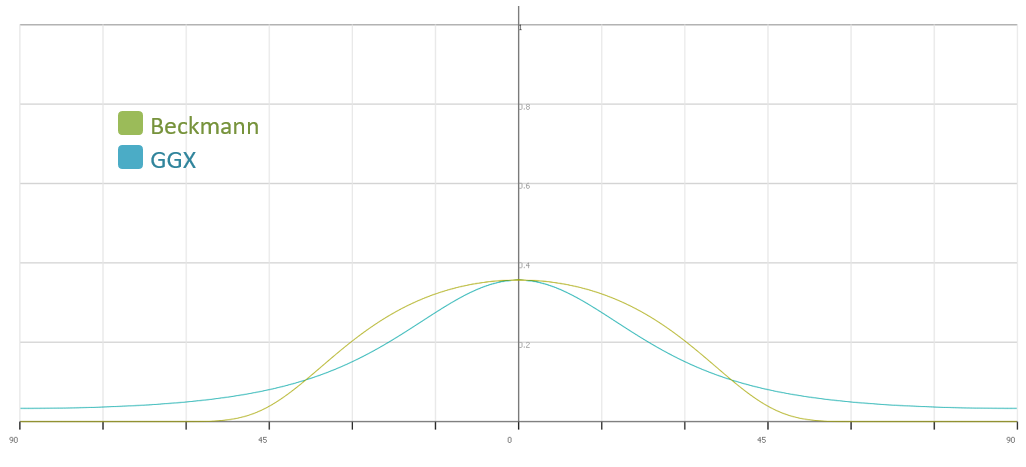
Figure 4: Logarithmic graph of NDF at roughness = 0.5, X-axis represents the angle between surface normal and microfacet normal (half vector), Y-axis represents the logarithmic of the resulting NDF
A more detailed explanation is found at the original paper of GGX by Walter et al.